Chapter 3 Data types and objects
All objects in R have a given type. You already know most of them, as these types are also used in mathematics. Integers, floating point numbers, or floats, matrices, etc, are all objects you are already familiar with. But R has other, maybe lesser known data types (that you can find in a lot of other programming languages) that you need to become familiar with. But first, we need to learn how to assign a value to a variable. This can be done in two ways:
or
there is almost no difference between these two approaches. You would need to pay attention to
this, and use <- in very specific situations to which you will very likely never be confronted
to.
Another thing you must know before going further is that you can convert from one type to another
using functions that start with as.(), such as as.character(), as.numeric(), as.logical(),
etc… For example, as.character(1) converts the number 1 to the character (or string) “1”.
There are also is.character(), is.numeric() and so on that test if the object is of the
required class. These functions exist for each object type, and are very useful. Make sure you
remember them!
3.1 The numeric class
To define single numbers, you can do the following:
The class() function allows you to check the class of an object:
## [1] "numeric"Decimals are defined with the character .:
3.2 The character class
Use " " to define characters (called strings in other programming languages):
## [1] "character"A very nice package to work with characters is {stringr}, which is also part of the {tidyverse}.
3.3 The factor class
Factors look like characters, but are very different. They are the representation of categorical
variables. A {tidyverse} package to work with factors is {forcats}. You would rarely use
factor variables outside of datasets, so for now, it is enough to know that this class exists.
We are going to manipulate factor variables in the next chatper 5.
3.4 The Date class
Dates also look like characters, but are very different too:
## [1] "2019-03-19"## [1] "Date"Manipulating dates and time can be
tricky, but thankfully there’s a {tidyverse} package for that, called {lubridate}. We are going
to go over this package in Chapter 5.
3.5 The logical class
This class is the result of logical comparisons, for example, if you type:
## [1] TRUER returns TRUE, which is an object of class logical:
## [1] "logical"In other programming languages, logicals are often called bools.
A logical variable can only have two values, either TRUE or FALSE.
3.6 Vectors and matrices
You can create a vector in different ways. But first of all, it is important to understand that a vector in most programming languages is nothing more than a list of things. These things can be numbers (either integers or floats), strings, or even other vectors.
3.6.1 The c() function
A very important function that allows you to build a vector is c():
This creates a vector with elements 1, 2, 3, 4, 5. If you check its class:
## [1] "numeric"This can be confusing: you where probably expecting a to be of class vector or
something similar. This is not the case if you use c() to create the vector, because c()
doesn’t build a vector in the mathematical sense, but rather a list with numbers.
Checking its dimension:
## NULLreturns NULL because a list doesn’t have a dimension,
that’s why the dim() function returns NULL. If you want to create a true vector, you need to
use cbind() or rbind().
3.6.2 cbind() and rbind()
You can create a true vector with cbind():
Check its class now:
## [1] "matrix"This is exactly what we expected. Let’s check its dimension:
## [1] 1 5This returns the dimension of a using the LICO notation (number of LInes first, the number of COlumns).
It is also possible to bind vectors together to create a matrix.
Now let’s put vector a and b into a matrix called matrix_c using rbind().
rbind() functions the same way as cbind() but glues the vectors together by rows and not by columns.
## [,1] [,2] [,3] [,4] [,5]
## [1,] 1 2 3 4 5
## [2,] 6 7 8 9 103.6.3 The matrix class
R also has support for matrices. For example, you can create a matrix of dimension (5,5) filled
with 0’s with the matrix() function:
If you want to create the following matrix:
\[ B = \left( \begin{array}{ccc} 2 & 4 & 3 \\ 1 & 5 & 7 \end{array} \right) \]
you would do it like this:
The option byrow <- TRUE means that the rows of the matrix will be filled first.
You can access individual elements of matrix_a like so:
## [1] 0and R returns its value, 0. We can assign a new value to this element if we want. Try:
and now take a look at matrix_a again.
## [,1] [,2] [,3] [,4] [,5]
## [1,] 0 0 0 0 0
## [2,] 0 0 7 0 0
## [3,] 0 0 0 0 0
## [4,] 0 0 0 0 0
## [5,] 0 0 0 0 0Recall our vector b:
To access its third element, you can simply write:
## [1] 8I have heard many people praising R for being a matrix based language. Matrices are indeed useful, and statisticians are very used to working with them. However, I very rarely use matrices in my day to day work, and prefer an approach based on data frames (which will be discussed below). This is because working with data frames makes it easier to use R’s advanced functional programming language capabilities, and this is where R really shines in my opinion. Working with matrices almost automatically implies using loops and all the iterative programming techniques, à la Fortran, which I personally believe are ill-suited for interactive statistical programming (as discussed in the introduction).
3.7 The list class
The list class is a very flexible class, and thus, very useful. You can put anything inside a list,
such as numbers:
or other lists constructed with c():
you can also put objects of different classes in the same list:
and of course create list of lists:
To check the contents of a list, you can use the structure function str():
## List of 3
## $ :List of 2
## ..$ : num 3
## ..$ : num 2
## $ :List of 2
## ..$ : num [1:2] 1 2
## ..$ : num [1:2] 3 4
## $ :List of 3
## ..$ : num 3
## ..$ : num [1:2] 1 2
## ..$ : chr "lists are amazing!"or you can use RStudio’s Environment pane:
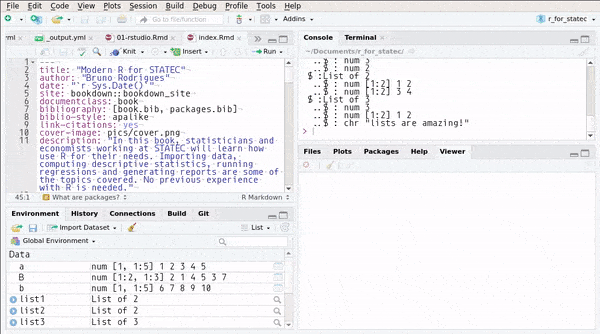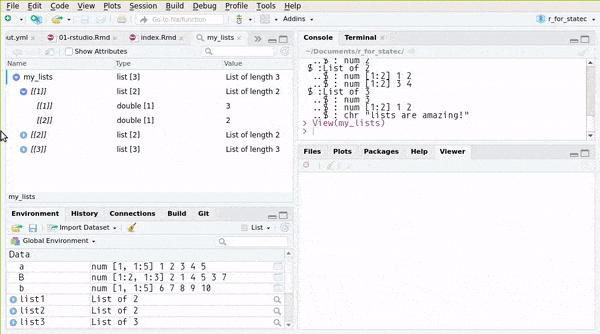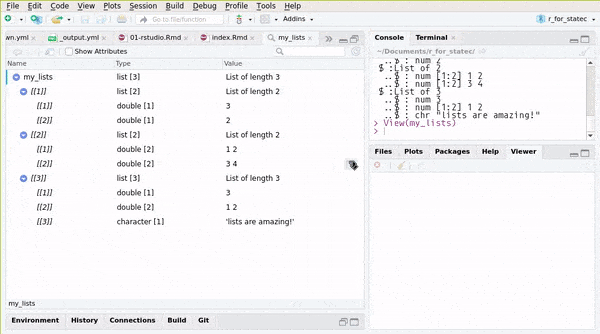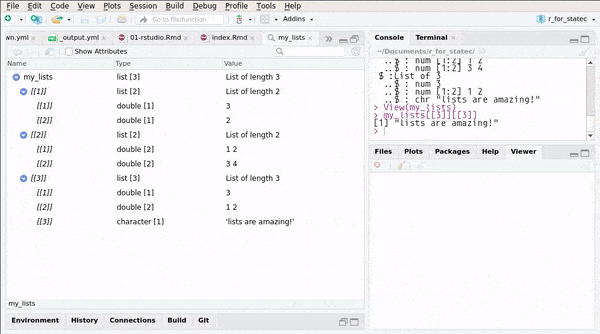
You can also create named lists:
and you can access the elements in two ways:
## [1] 2or, for named lists:
## [1] "this is a named list"Lists are used extensively because they are so flexible. You can build lists of datasets and apply functions to all the datasets at once, build lists of models, lists of plots, etc… In the later chapters we are going to learn all about them. Lists are central objects in a functional programming workflow for interactive statistical analysis.
3.8 The data.frame and tibble classes
In the next chapter we are going to learn how to import datasets into R. Once you import data, the
resulting object is either a data.frame or a tibble depending on which package you used to
import the data. tibbles extend data.frames so if you know about data.frame objects already,
working with tibbles will be very easy. tibbles have a better print() method, and some other
niceties. If you want to know more, I go into more detail in my other
book
but for our purposes, there’s not much you need to know about data.frame and tibble objects,
apart that this is the representation of a dataset when loaded into R.
However, I want to stress that these objects are central to R and are thus very important; they are
actually special cases of lists, discussed above. There
are different ways to print a data.frame or a tibble if you wish to inspect it. You can use
View(my_data) to show the my_data data.frame in the View pane of RStudio:
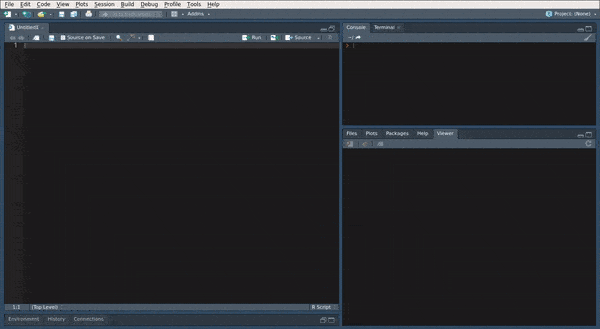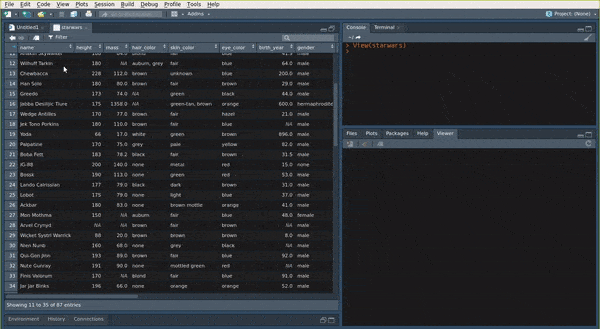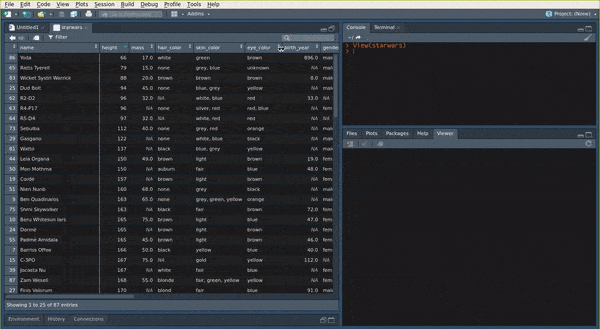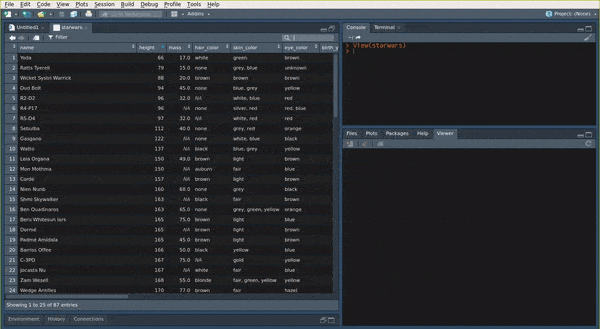
You can also use the str() function:
And if you need to access an individual column, you can use the $ sign, same as for a list:
3.9 Formulas
We will learn more about formulas later, but because it is an important object, it is useful if you already know about them early on. A formula is defined in the following way:
## [1] "formula"Formula objects are defined using the ~ symbol. Formulas are useful to define statistical models,
for example for a linear regression:
or also to define anonymous functions, but more on this later.
3.10 Models
A statistical model is an object like any other in R:
## [1] "lm"my_model is an object of class lm. You can apply different functions to a model object:
##
## Call:
## lm(formula = mpg ~ hp, data = mtcars)
##
## Residuals:
## Min 1Q Median 3Q Max
## -5.7121 -2.1122 -0.8854 1.5819 8.2360
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 30.09886 1.63392 18.421 < 2e-16 ***
## hp -0.06823 0.01012 -6.742 1.79e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.863 on 30 degrees of freedom
## Multiple R-squared: 0.6024, Adjusted R-squared: 0.5892
## F-statistic: 45.46 on 1 and 30 DF, p-value: 1.788e-07This class will be explored in later chapters.
3.11 The is.*() and as.*() functions
is.*() and as.*() are very powerful, and this is the right moment to introduce them. is.*()
test the class of an object:
## [1] FALSE## [1] FALSEas.*() functions convert from one type to another:
## [1] "7"## [1] 23.12but only if it makes sense:
## Warning: NAs introduced by coercion## [1] NAKeep these in mind, because they are going to be very useful. The {purrr} package introduces
similar functions, is_*() and as_*(). We will explore them in Chapter 9.
3.12 Exercises
Exercise 1
Try to create the following vector:
\[a = (6,3,8,9)\]
and add it this other vector:
\[b = (9,1,3,5)\]
and save the result to a new variable called result.
Exercise 2
Using a and b from before, try to get their dot product.
Try with a * b in the R console. What happened?
Try to find the right function to get the dot product. Don’t hesitate to google the answer!
Exercise 3
How can you create a matrix of dimension (30,30) filled with 2’s by only using the function matrix()?
Exercise 4
Save your first name in a variable a and your surname in a variable b. What does the function:
do? Look at the help for paste() with ?paste or using the Help pane in RStudio. What does the
optional argument sep do?
Exercise 5
Define the following variables: a <- 8, b <- 3, c <- 19. What do the following lines check?
What do they return?
Exercise 6
Define the following matrix:
\[ \text{matrix_a} = \left( \begin{array}{ccc} 9 & 4 & 12 \\ 5 & 0 & 7 \\ 2 & 6 & 8 \\ 9 & 2 & 9 \end{array} \right) \]
- What does
matrix_a >= 5do? - What does
matrix_a[ , 2]do? - Can you find which function gives you the transpose of this matrix?
Exercise 7
Solve the following system of equations using the solve() function:
\[ \left( \begin{array}{cccc} 9 & 4 & 12 & 2 \\ 5 & 0 & 7 & 9\\ 2 & 6 & 8 & 0\\ 9 & 2 & 9 & 11 \end{array} \right) \times \left( \begin{array}{ccc} x \\ y \\ z \\ t \\ \end{array}\right) = \left( \begin{array}{ccc} 7\\ 18\\ 1\\ 0 \end{array} \right) \]
Exercise 8
Load the mtcars data (mtcars is include in R, so you only need to use the data() function to
load the data):
if you run class(mtcars), you get “data.frame”. Try now with typeof(mtcars). The answer is now
“list”! This is because the class of an object is an attribute of that object, which can even
be assigned by the user:
## [1] "don't do this"The type of an object is R’s internal type of that object, which cannot be manipulated by the user.
It is always useful to know the type of an object (not just its class). For example, in the particular
case of data frames, because the type of a data frame is a list, you can use all that you learned
about lists to manipulate data frames! Recall that $ allowed you to select the element of a list
for instance:
## [1] 1Because data frames are nothing but fancy lists, this is why you can access columns the same way:
## [1] 21.0 21.0 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 17.8 16.4 17.3 15.2 10.4 10.4 14.7 32.4 30.4 33.9 21.5 15.5
## [23] 15.2 13.3 19.2 27.3 26.0 30.4 15.8 19.7 15.0 21.4